Firma digital: un esquema de firma basado en curvas elípticas

En la era digital, la autenticidad, integridad y no repudio de los documentos digitales son los requisitos básicos para lograr la seguridad de la información. La firma digital es una de las principales formas de cumplir con los requisitos anteriores, y también es uno de los contenidos de investigación de la criptografía moderna.

¿Cuáles son las formas de las firmas digitales? ¿Cuáles son las ventajas de las firmas digitales basadas en criptografía? ¿Cuáles son los esquemas de implementación de firma digital comúnmente utilizados? ¿Qué tipo de riesgos se esconden en el proceso de uso? Comenzaremos por comprender el concepto y luego lo introduciremos paso a paso.

Enciclopedia Blockchain No.34: Basado en el esquema de firma de curva elíptica

Con la mejora continua de las capacidades de procesamiento de información de la computadora, los requisitos de longitud de clave también son cada vez más altos.Este problema es particularmente importante para los sistemas con capacidad de almacenamiento limitada.

La propuesta de la Criptografía de Curva Elíptica (ECC) ha cambiado esta situación, pudiendo proporcionar una seguridad equivalente o superior a la de otros sistemas con claves más cortas, y se ha convertido en un sistema de cifrado seguro, eficaz y ampliamente utilizado que ha sido probado hasta el momento. Tres criptosistemas de clave pública. Este artículo continuará introduciendo esquemas de firma digital basados ​​en curvas elípticas.

Las curvas elípticas se han estudiado ampliamente en álgebra y geometría durante 150 años y tienen una base teórica sólida.

La llamada curva elíptica se refiere a la ecuación de Weierstrass:

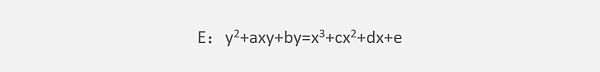
La curva plana determinada, en la que a, b, c, d, e pertenecen al campo F, que puede ser el campo de números racionales Q, el campo de números complejos C o el campo finito GF(p).

Una curva elíptica es una colección de todos los puntos (x, y) en ella, más un punto infinito O (que define un punto especial en la curva elíptica, denotado como O, que es un punto en el infinito en el plano afín, llamado infinito punto .En el plano xOy, se puede considerar como una abstracción del conjunto de todas las líneas rectas paralelas al eje y).

Las curvas elípticas en campos finitos se usan comúnmente en criptografía, lo que significa que en la definición de ecuaciones de curvas elípticas, todos los coeficientes son elementos en un cierto campo finito GF(p). Su fórmula más simple es:

Solo hay un número finito de puntos discretos en la curva elíptica, establezca N, entonces N se llama el orden de la curva elíptica como N. Cuanto mayor sea N, mayor será la seguridad. En base a esto, una representación gráfica de una curva elíptica se puede representar de la siguiente manera:

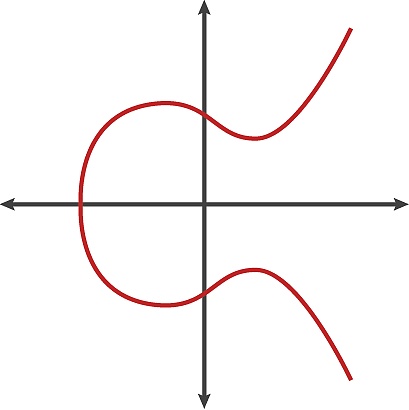
Por supuesto, existen otras representaciones de curvas elípticas basadas en diferentes valores de variables:

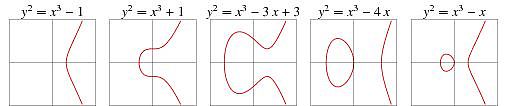
Cuando observamos cuidadosamente estas curvas, podemos encontrar algunas propiedades interesantes: (1) simetría, es decir, cualquier punto de la curva puede reflejarse en el eje x y mantener la curva sin cambios; (2) cualquier línea no perpendicular y curva Hay como máximo tres intersecciones.

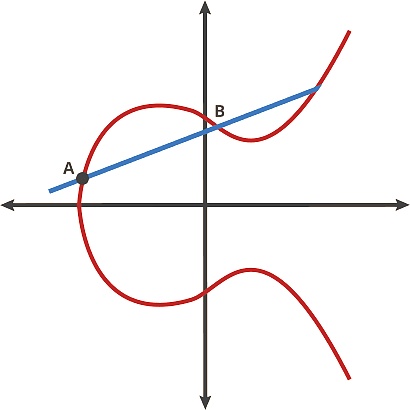
Podemos pensar en esta curva como un juego de billar. Tome dos puntos cualquiera de la curva y dibuje una línea a través de ellos, que se cruzará con la curva en otra ubicación. En este juego de billar, tomas una pelota en el punto A, la lanzas hacia el punto B y, cuando llega a la curva, la pelota rebota hacia arriba (si está debajo del eje x) o hacia abajo (si está arriba de la x). -eje) al otro lado de la curva. Podemos pensar en la pelota moviéndose entre dos puntos, y dos puntos cualquiera en la curva chocan para obtener un nuevo punto.

A·B = C

O puede usar un cierto punto para colisionar continuamente consigo mismo para crear nuevos puntos.

A · A = B

A · C = D

…

En este proceso, un punto inicial obtendrá el punto final después de n operaciones, cuando solo se conocen los valores de estos dos puntos, es difícil encontrar n.

Es como una persona que juega un juego de billar durante un período de tiempo aleatorio en una habitación, y es fácil para él golpear la pelota una y otra vez siguiendo las reglas descritas anteriormente. Pero si alguien entra en la habitación y la pelota simplemente termina en un punto, incluso si conoce todas las reglas del juego y dónde comenzó la pelota, no puede estar seguro de cuántos golpes recibió la pelota allí. Es fácil de calcular hacia adelante y difícil de calcular hacia atrás, que también es la base de la función de trampilla.

En 1985, Koblitz y Miller introdujeron la curva elíptica en la criptografía y propusieron un grupo de conjuntos de puntos sobre la curva elíptica basados ​​en el campo finito GF(p).En este grupo se definió el problema del logaritmo discreto y una clase de algoritmos públicos. El criptosistema clave es un criptosistema discreto basado en curvas elípticas, y su seguridad se basa en la intratabilidad del problema del logaritmo discreto en curvas elípticas.

Tomamos el esquema de implementación de la firma digital ECDSA basado en la curva elíptica como ejemplo para ilustrar su proceso de implementación específico.

Algoritmo de generación de claves

Supongamos que GF(p) es un campo finito y E es una curva elíptica en el campo finito GF(p). Seleccione un punto G∈E en E, y el orden de G es un número primo n que cumple con los requisitos de seguridad, es decir, nG=O (O es un punto en el infinito).

Elija un número aleatorio d, d ∈ [1, n-1], calcule Q, de modo que Q=dG. Entonces la clave pública es (n, Q) y la clave privada es d.

Algoritmo de firma

Suponiendo que el mensaje a firmar es m, tras el siguiente proceso de cálculo, la firma digital del firmante para el mensaje m es (r, s).

Algoritmo de autenticación

El proceso de verificación del destinatario de la firma B para la firma del mensaje m (r, s) es el siguiente:

Juzgue la relación entre r y r1, si son iguales, la firma es válida; de lo contrario, la firma no es válida.

Además del esquema ECDSA presentado anteriormente, existen muchos esquemas de firma digital basados ​​en elipses, y otros esquemas similares a DSA, como Schnorr y EIGamal, también se han trasplantado a grupos finitos de curva elíptica.

De la introducción anterior, podemos ver que la seguridad de las firmas digitales depende del problema del logaritmo discreto en grupos finitos basados ​​en curvas elípticas.

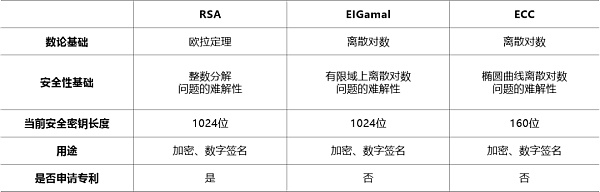
En comparación con la firma digital RSA y la firma digital basada en el logaritmo discreto de campo finito mencionadas en el capítulo anterior, el esquema de firma digital basado en la curva elíptica tiene las siguientes características: Bajo las mismas condiciones de fuerza de seguridad, la longitud de la firma es corta, el espacio de almacenamiento clave es pequeño y es adecuado para ocasiones en las que el espacio de almacenamiento es limitado, el ancho de banda es limitado y se requiere una implementación de alta velocidad.

Además, los recursos de curvas elípticas son abundantes y hay una gran cantidad de curvas elípticas diferentes en el mismo campo finito, lo que también agrega garantías adicionales para la seguridad.

Es precisamente porque la curva elíptica tiene una estructura de grupo rica y selectividad múltiple, y puede acortar en gran medida la longitud de la clave mientras mantiene la misma seguridad que los sistemas RSA y EIGamal, por lo que tiene un escenario de aplicación más amplio.

Tags：

Binance APP