¿Cuál es la relación entre la constante natural e y el consenso esperado de Filecoin?

Lao Tse dijo: "El hombre sigue a la tierra, la tierra sigue al cielo, el cielo sigue al Tao y el Tao sigue a la naturaleza". En la práctica de la cadena de bloques, dado que se establece el sistema Code is Law, sigue las reglas de In Math We Trust. En una red que no está controlada por individuos, es especialmente importante seguir las leyes de la naturaleza. Abogo por que el diseño de Filecoin sea simple y natural. Esta es también la razón.

La constante natural e es un número mágico, y es extremadamente natural en matemáticas. Este artículo habla sobre la relación entre la evolución del mecanismo de consenso de Filecoin y la constante natural e.

La tasa inicial esperada de bloques vacíos por consenso es demasiado alta: 1/e

La realización del consenso esperado es un proceso de descubrimiento continuo

Se espera que aumente el número de bloques de conjuntos de consejos (a 5), ​​teniendo en cuenta tanto la seguridad como la eficiencia.

Votar cada byte: elegante lotería criptográfica + e

[Advertencia: Matemáticas, Probabilidad y Distribución]

e se llama una constante de la naturaleza, ya los ojos de los matemáticos, esta constante es muy natural. Sin embargo, para la gente común, es difícil de entender porque no hay una descripción visual. A través de la aplicación de e en Filecoin, este artículo espera encontrar algunos puntos que puedan ayudar a todos a 1) comprender algunos diseños de Filecoin; 2) obtener una pequeña descripción visual e impresión de e a través de Filecoin.

Hay dos constantes matemáticas comunes, complejas e interesantes, una es π y la otra es e. Todo el mundo está muy familiarizado con π porque tiene un nombre muy visual llamado pi, que significa la relación entre la circunferencia y el diámetro de cualquier círculo. Muy vívido, muy fácil de entender. Si no lo aprendes en la escuela primaria, siempre lo aprenderás en la escuela secundaria.

De hecho, e es una constante matemática tan importante como π, y su uso en matemáticas no es menor que el de π. Por ejemplo, en la cadena de bloques de Filecoin que estamos discutiendo hoy, e se usa en muchos lugares, pero π no, básicamente no se usa.

π = 3.1415926535897...... 

e = 2.718281828459045...

Tanto π como e son números trascendentales, es decir, no son números algebraicos (soluciones de ecuaciones de números racionales), y por supuesto también son números irracionales, infinitos decimales no periódicos.

Pero, de hecho, e y π tienen una relación muy estrecha en matemáticas. Incluso se puede decir que e es otra representación de π. Por favor, vea la fórmula matemática más elegante: la fórmula de Euler:

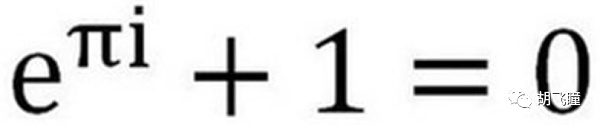
¿Por qué es elegante? Esta sencilla fórmula unifica los cinco elementos (0, 1, i, π, e) en matemáticas de forma muy sencilla. Así como los físicos quieren unificar campos de fuerza, los matemáticos también tienen la paranoia de resumir leyes concisas.

Esta fórmula también expresa una relación simple y directa entre e y π. Por supuesto, hay algunas relaciones interesantes entre ellos, tales como:

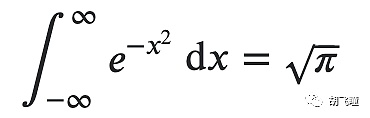
La billetera cifrada Exodus recauda $60 millones a través de la venta de acciones: Jinse Finance informó que desde el 8 de abril, la billetera criptográfica Exodus ha recaudado $60 millones a través de la venta de acciones de la compañía. Noticias anteriores, Exodus ha sido aprobado por la SEC de EE. UU., lo que le permite ofrecer acciones ordinarias Clase A de acuerdo con las regulaciones RegA+. [2021/4/14 20:16:27]

Sin embargo, estos parecen complicar más las cosas y no son útiles para la comprensión de e en sí. ¿Qué diablos es e? En matemáticas, e es la base de los logaritmos naturales. Una de sus características generales es que la derivada de e^x sigue siendo e^x. A su vez, e puede expresarse y calcularse mediante la siguiente fórmula:

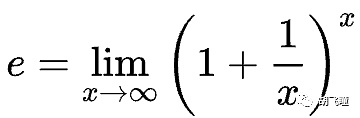
Una expresión un poco más vívida es que en el cálculo del interés compuesto, e expresa una tasa de interés que se duplica dentro de un período de tiempo y el valor límite que se puede lograr mediante el cálculo continuo del interés compuesto del límite. Es decir, si la tasa de interés anual es del 100%, si subdivides infinitamente un año en n períodos de tiempo, entonces la tasa de interés de cada período de tiempo es 1/n, y el ingreso que puedes obtener con intereses es e veces, es decir, un poco más de 2,7 veces.  

Esta imagen todavía no es suficiente, así que echemos un vistazo al mecanismo de consenso asignado a Filecoin.

Primero revisemos el consenso esperado descrito en el libro blanco de Filecoin. En la implementación inicial de go-filecoin, se adoptó un consenso esperado simple, es decir, cada minero obtiene la probabilidad de producir un bloque de acuerdo con la relación entre su poder de cómputo y el poder de cómputo total. Debido a que la suma del poder de cómputo de todos los mineros es igual al poder de cómputo total, el valor esperado de la probabilidad total de generación de bloques en cada ronda del sistema es 1. En pocas palabras, se produce un bloque en promedio en cada ronda, pero cada minero calcula de forma independiente, por lo que la cantidad de bloques producidos en cada ronda puede ser diferente.

Entonces, en este caso, construimos un modelo simple (y efectivo) para realizar una deducción. Asumiendo que el número de mineros en el sistema es n, y el poder de cómputo de cada minero es 1/n, entonces, en cada ronda, la probabilidad de que cada minero produzca un bloque es 1/n.

De esta forma, la probabilidad de que quede un bloque vacío en una ronda es: 

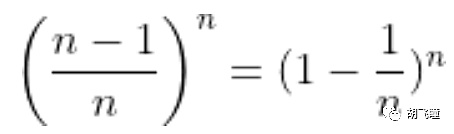
Si n es lo suficientemente grande, entonces, se puede obtener:

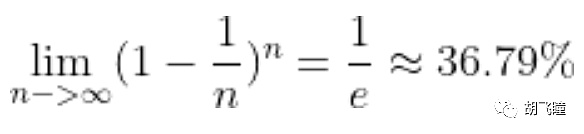
En otras palabras, la probabilidad de una rueda vacía es más de un tercio, lo cual es demasiado alto.

Entonces, ¿cuál es la probabilidad de que el número de bloques producidos sea 1? Simplemente puede hacer el siguiente cálculo:

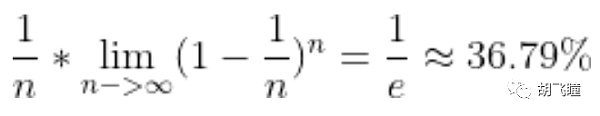
Todavía poco más de un tercio. La probabilidad restante de menos de un tercio son rondas de bloques múltiples. Esta conclusión es completamente consistente con la prueba de Devnet en ese momento.

A partir de aquí, hemos encontrado una explicación más visual para la constante natural e, es decir: en una elección de votación independiente con mucha gente (gran número) participando, todos tienen la misma probabilidad de ganar la elección, y al mismo tiempo se espera ganar Cuando el número de votantes es 1, la probabilidad de que no se obtenga el resultado de la elección es el recíproco de e, es decir, 1/e.

Simulamos la alta tasa de bloques vacíos en la red de desarrollo y la discutimos con el equipo de investigación y desarrollo de Filecoin. Obviamente, una proporción tan alta de rondas de bloques vacíos no es buena, porque el tiempo de bloque no es fijo y el tiempo de transacción es difícil de predecir.

Entonces, ¿qué es un cambio fácil? Eso es aumentar el número esperado de bloques en cada ronda. Debido a que se espera que puedan aparecer múltiples bloques en una ronda de consenso, y la combinación de tipsset se adopta en la implementación, por lo que aumentar la cantidad esperada de bloques es muy simple para el diseño y la implementación.

Antes de la red de prueba, la implementación de Filecoin introdujo el concepto de la cantidad esperada de bloques por ronda, que se define como E (ExpectedBlocksPerEpoch). Valor predeterminado actual: E=5

Ahora que la cantidad esperada de bloques ha aumentado, la forma más fácil es aumentar 5 veces la probabilidad de generación de bloques de cada minero. Sin embargo, el cálculo de la producción de bloques del minero adopta el método de tirar los dados. Eso es generar un número en un espacio de 256 bits para comparar la proporción de su propio poder de cómputo, para juzgar si tiene derecho a producir bloques. Hay un problema de datos fuera de los límites aquí. La realización de Filecoin ha pasado por tres etapas en este juicio:

Fase 1: Cada minero se divide según su propio poder de cómputo, y elige según una parte más pequeña, y si gana la elección, obtendrá un voto. La misma potencia informática predeterminada se divide uniformemente cada 25 sectores (la parte restante se calcula por separado). La ventaja de este método es que cada elector tiene básicamente el mismo poder de cómputo y se lleva a cabo una elección justa. Sin embargo, dado que cada 25 sectores deben calcularse por separado, cada parte requiere acceso de E/S, lo que consume mucho tiempo. El propósito original del equipo de Filecoin era reunir el derecho a generar bloques y pruebas de espacio-tiempo. Sin embargo, al final, desde la perspectiva de la seguridad, debido al cálculo relativamente complicado, se abandonó.

Etapa 2: simplificación extrema directa, independientemente del problema de cruzar el límite, multiplicar directamente por 5 para comparación y cálculo. Esta es una simplificación en el caso de que la prueba de espacio-tiempo haya reemplazado a SurprisedPoSt por WindowedPoSt. Sin embargo, hay dos problemas al hacer esto: 1) Los mineros con un poder de cómputo superior al 20% definitivamente sufrirán; 2) Cuando el poder de cómputo de los mineros sea lo suficientemente grande, definitivamente podrán ganar la elección. Este segundo problema es más serio. Proponemos solemnemente que este es un problema de seguridad y debe cambiarse.

Fase 3: Adopte el método de lotería criptográfica y aprenda del algoritmo adoptado por Algorand. Avanza gradualmente hacia la perfección.

La lotería criptográfica de Algorand es una muy buena aplicación de distribución de probabilidad para las elecciones, y es excelente para las redes de POS de cadena de bloques. Es relativamente simple y fácil de implementar. El algoritmo específico es el siguiente:

Aquí no se da una explicación detallada, y aquellos que la necesiten pueden solicitar información relevante. En pocas palabras, durante el proceso de elección de POS, cuando realiza un sorteo con los números aleatorios verificables que genera, puede juzgar en qué intervalo se encuentra en función de su propia participación y la distribución binomial correspondiente.Cuántos votos se recibieron.

La distribución binomial es una distribución en la que n veces independientes de la misma probabilidad se calculan por separado y luego se suman, y toda la distribución simplemente corta todo el espacio de probabilidad. Por lo tanto, solo necesita mirar el espacio donde está su número aleatorio verificable (esta parte es más difícil de explicar claramente, y aquellos que estén interesados ​​​​lo discutirán fuera de línea).

Entonces, para Filecoin, la participación en la elección es su poder de cómputo. Si se puede subdividir aún más de acuerdo con el método de la fase 2 mencionado anteriormente, se puede considerar que participa en la votación de cada byte. De esta forma, el número de electores que participan en la votación es muy grande y no es necesario utilizar la distribución binomial para todo el cálculo, sino que se puede calcular mediante la distribución de Poisson. La fórmula de cálculo de la distribución de Poisson es la siguiente:

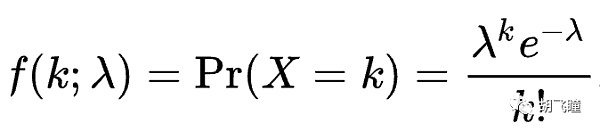
Aquí λ es el producto de la propia participación y el número total esperado de votos electorales. En Filecoin, es

 E * mPow/totPow; k es el número de votos obtenidos.

Mira la fórmula anterior, ¿no es increíble? La constante natural e se utiliza una vez más en el cálculo de la elección de Filecoin. El uso de la distribución de Poisson para el cálculo es una mejora de Filecoin, que es muy consistente con las características de Filecoin, y el cálculo también es muy simple.  

Después de que se adopte la lotería criptográfica, no hay garantía de que los mineros obtengan el derecho a producir bloques en cada ronda. Esto es normal, porque todos tiran los dados por sí mismos y el cálculo del derecho a producir bloques es independiente. En este caso, ¿cuál es la probabilidad de ganar diferentes votos en bloque en cada ronda? Una simple simulación da como resultado la siguiente tabla:

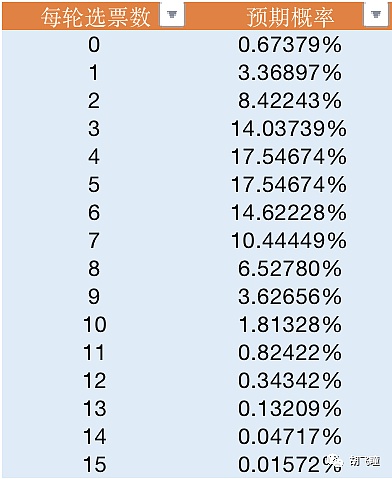
Aquí la probabilidad de una ronda vacía es e^-5.

Dicho esto, espere una rueda vacía a menos de 200 altitudes. Se ve bien. El número de votos en cada ronda es 3, 4, 5, 6 y 7. La distribución es cada vez más pareja. También hay muchos casos en los que el número de votos llega a 15, alrededor de 1,6 de 10.000.

Al ver esto (si realmente tienes paciencia para ver esto), quizás te preguntes si e tiene una mayor relación con la probabilidad, de hecho, puedo decirte que π se usa a veces en los cálculos de probabilidad. Porque estas dos constantes tienen una relación ambigua.

El uso de la constante natural e en las elecciones hasta ahora parece muy natural y elegante.

Al mismo tiempo, Filecoin también usa e para los cálculos en la liberación de tokens. Este no tiene nada que ver con la probabilidad, sino con la decadencia. Filecoin no libera Token mediante la reducción periódica a la mitad, sino que imita la descomposición radiactiva, es decir, la descomposición exponencial. El libro blanco está diseñado para reducirse a la mitad en 6 años. En general, la fórmula para la atenuación se puede escribir como:

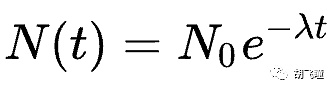
La fórmula anterior se puede entender como: el Token inicial es N0, y con el paso del tiempo, el sistema libera, y la fórmula de cálculo de la cantidad de Token N(t) que debe retenerse en el sistema en el momento t.

Mira aquí, la constante natural e aparece de nuevo. Por supuesto, no es necesario usar e aquí. Pero dado que e se usa ampliamente, es conveniente y conveniente de usar. Entonces, básicamente, ahora este es un uso unificado.

Tags：

Uniswap