Algoritmo aleatorio de Ethereum 2.0

Introducción

Si estás tratando de aprender el baile aleatorio, estás en el lugar equivocado. Pero créanme, mezclar en Eth2 es igual de emocionante.

La lista aleatoria es una operación básica en Ethereum 2.0. Se utiliza principalmente para seleccionar verificadores pseudoaleatoriamente para formar comités en cada intervalo de 12 segundos y para seleccionar proponentes para bloques de cadena de balizas en cada intervalo.

Shuffle parece bastante sencillo. Aunque tiene algunas trampas a tener en cuenta, estas trampas se entienden muy bien en informática. El patrón oro es probablemente la combinación Fisher-Yeats. Entonces, ¿por qué no lo usamos en Eth2? Lo explicaré en detalle al final del artículo, pero en resumen: cliente ligero.

El algoritmo de barajado que usamos es swap-or-not, no Fisher-Yates. Esta elección se basa en el papel que se usó originalmente para construir el esquema de cifrado. Recientemente reescribí nuestra implementación en el cliente Eth2 Teku, así que quería escribirlo mientras estaba caliente.

Algoritmo de barajado de intercambio o no

Una ronda de proceso de operación

Los shuffles se realizan en rondas. El proceso es el mismo para cada ronda, así que solo demostraré el proceso para una ronda a continuación, que es mucho más simple de lo que parece.

Elija un punto de pivote y encuentre el primer índice de espejo

Primero, elegimos un índice de pivote p, que se selecciona pseudoaleatoriamente en función de las rondas y algunos otros datos iniciales. Después de seleccionar el eje, se fija en la ronda.

Con base en este punto de pivote, seleccionamos un índice de espejo m1 en el punto medio entre p y 0, es decir, m1=p/2. (En aras de la explicación, ignoraremos el problemático problema de redondeo de errores uno por uno)

Punto de pivote e índice del primer espejo

Desde el índice del primer espejo hasta el punto de pivote, con reemplazo o no

Para cada índice entre el índice espejo m1 y el índice pivote p, decidimos aleatoriamente si reemplazamos esos elementos.

Por ejemplo, para el índice i1, si elegimos no reemplazar, continuamos seleccionando el siguiente índice.

Si decidimos reemplazar, reemplazamos el elemento de la lista en i1 con el de i1', su imagen en el índice espejo. Es decir, i1 se reemplaza por i1'=m1-(i1-m1), de modo que las distancias de i1 e i1' a m1 son iguales.

Tomamos la misma decisión de cambiar o no para cada índice entre m1 y p.

decisión de cambiar o no desde el primer índice espejo hasta el pivote

Calcule el índice del segundo espejo

Después de tomar todas las decisiones de índice de m1 a p, ahora encontramos el segundo índice de espejo con m2 como punto medio, es decir, el punto que es equidistante de p y el final de la lista. Eso es m2=m1+n/2.

Índice del segundo espejo

Del punto pivote a la segunda imagen especular, con reemplazo o no

Finalmente, repetimos el proceso de intercambio o no, considerando todas las decisiones de reemplazo de punto a pivote p, es decir, decisiones de p al segundo espejo m2. Si elegimos no reemplazar, pasamos al siguiente. Si elegimos reemplazar, reemplazamos el elemento en j1 ​​con su imagen especular en j1 'en el índice espejo m2.

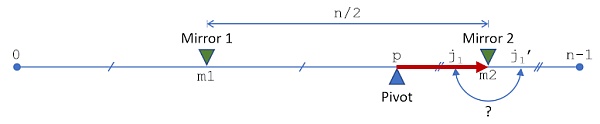
decisión de cambiar o no del pivote al índice del segundo espejo

Combinado

Al final de una ronda, hemos considerado todos los índices entre m1 y m2, es decir, la mitad de todos los índices, y cada índice tiene un índice específico en la otra mitad, ya sea que se reemplace o no. Así, con respecto a la sustitución o no, todos los índices se han considerado una vez.

La siguiente ronda comienza con rondas crecientes (o decrecientes) para que tengamos un nuevo índice de pivote, y luego comienza a recorrer el proceso descrito anteriormente.

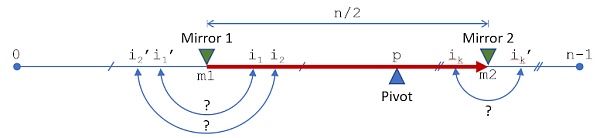
El proceso de pasar de un espejo a otro en la misma ronda.

Qué es interesante

Lugar inteligente

Al decidir si reemplazar o no, el algoritmo elige inteligentemente el índice candidato más alto o su imagen especular. Significa que cuando está debajo del eje, se selecciona i_1 en lugar de i_1', cuando está arriba del eje, se selecciona i_k' en lugar de i_k. Esto significa que podemos iterar sobre los índices en la lista de manera flexible: podemos separar 0 a m1 y p a m2 en dos bucles separados, o combinar ambos en el mismo bucle de m1 a m2, como lo describí anteriormente (e implementé ) en este papel. El resultado es el mismo en ambos sentidos: no importa si considero i_1 o espejo i_1'; la sustitución o no da el mismo resultado.

Redondo

En Eth2, el proceso anterior se realizará 90 veces. El documento original menciona que se necesitan rondas de 6lgN para "comenzar a mostrar un buen margen de seguridad en los ataques criptográficos selectivos (CCA)", donde N es la longitud de la lista. En la especificación comentada de Vitalik, dijo que "los expertos en criptografía sugieren que podemos proporcionar suficiente seguridad con rondas de 4log2N".

El número máximo absoluto de validadores en Eth2, que es el número máximo de veces que necesitamos barajar la lista, es de unos 222 (4,2 millones). El valor estimado dado por Vitalik es de 88 rondas y el valor estimado en el documento es de 92 rondas (suponiendo que lg es el logaritmo natural). Así que ahora estamos en un rango más o menos correcto, especialmente porque es muy probable que no terminemos con tantos validadores activos.

Ajustar las rondas en función de la longitud de la lista podría tener resultados interesantes, pero no lo haríamos, podría ser una optimización innecesaria.

Curiosamente, cuando Least Authority auditó la especificación de Beacon Chain, inicialmente encontraron que había un sesgo en el barajado que selecciona a los proponentes de bloques (ver Problema F). Pero resultó que por error usaron una configuración aleatoria con solo 10 rondas. Cuando aumentaron la configuración aleatoria a 90 rondas (el número que usamos en la red principal), el sesgo desapareció.

(pseudo)aleatorio

El algoritmo de barajado requiere que elijamos aleatoriamente un punto de pivote en cada ronda y elijamos aleatoriamente si reemplazamos cada elemento en cada ronda.

En Eth2, definitivamente generamos aleatoriedad a partir de un valor semilla, por lo que la misma semilla siempre producirá el mismo resultado de barajado.

El índice pivote se genera realizando un hash SHA2 de 8 bytes en la semilla concatenada con la ronda, y el índice pivote es generado por los ocho bytes del hash SHA2 del valor semilla, que está concatenado con la ronda, por lo que generalmente cambia cada ronda.

Los bits decisivos utilizados para decidir si reemplazar un elemento se extraen de los siguientes elementos: el hash SHA256 de la semilla, la ronda, el índice del elemento en la lista.

Eficiencia

Este algoritmo de barajado es mucho más lento que el algoritmo de Fisher-Yates. Si el algoritmo de Fisher-Yates requiere N mezclas, nuestro algoritmo requiere un promedio de 90N/4 mezclas. También tenemos que considerar la generación de pseudoaleatoriedad, que es la parte más cara del algoritmo. Fisher-Yates necesita una aleatoriedad cercana a Nlog2N dígitos, y necesitamos 90(log2N+N/2) dígitos De acuerdo con el rango de valores de N que necesitamos en Eth2, el exceso de dígitos es bastante (cuando N es un millón , Eth2 necesita aproximadamente el doble de N).

¿Por qué elegir el algoritmo swap-or-not?

Si no es eficiente, ¿por qué elegiría esta implementación?

Mezclar un solo elemento

El punto brillante de este algoritmo es que si solo nos preocupamos por unos pocos índices, no necesitamos calcular la mezcla de toda la lista. De hecho, podemos usar este algoritmo en un solo índice para averiguar qué índice se reemplazará.

Entonces, si queremos saber dónde se ha barajado el elemento en el índice 217, podemos ejecutar el algoritmo solo para ese índice, sin barajar la lista completa. Además, a la inversa, si quisiéramos saber qué elemento se barajó en el índice 217, podríamos ejecutar el algoritmo a la inversa para encontrar el elemento 217 (inverso significa ejecutar las rondas de mayor a menor, no de menor a mayor).

En resumen, podemos calcular dónde se barajó el elemento i y de dónde vino el elemento i (usando la operación inversa) en tiempo constante, y el tiempo de cálculo no depende de la longitud de la lista. Fisher-Yates shuffle no tiene esta propiedad y no puede mezclar un solo índice, a menudo necesitan mezclar repetidamente la lista completa.

Lo que está escrito en la especificación Eth2 es cómo se aplica el algoritmo para barajar un solo índice. De hecho, mezclar toda la lista a la vez es solo una optimización de la misma. Si quisiéramos, podríamos barajar solo un elemento de la lista a la vez: (a la inversa) ejecutar el barajado para encontrar qué elemento terminó en el índice 0, ejecutar otro barajar para encontrar qué elemento terminó en el índice 1, y así sucesivamente.

La razón por la que no hacemos eso se debe simplemente a la decisión de que intercambiar o no necesita generar un hash de 256 bits a la vez, y tirar 255 bits de esa manera sería un desperdicio. Si usamos un oráculo o hash de 1 bit, barajar un elemento de la lista es tan eficiente como barajar la lista completa.

Sé un verdadero cliente "light"

La razón por la que esta función tiene sentido tiene que ver con los clientes ligeros. Los clientes ligeros son equivalentes a los observadores de la cadena de balizas y la cadena de fragmentos Eth2. No almacenan el estado completo, pero esperan acceder de forma segura a los datos de la cadena. Un paso necesario para verificar que sus datos son correctos, es decir, que no se ha producido ningún fraude, es el cálculo del comité que da fe de los datos.

Es decir, se utiliza el algoritmo de barajar y no queremos que el cliente ligero tenga que almacenar o barajar toda la lista de validadores. Al cambiar o no mezclar, solo pueden hacer cálculos sobre un pequeño subconjunto de los miembros del comité que necesitan, lo que mejorará en gran medida la eficiencia general.

Historia

Si te gusta la naturaleza arqueológica de GitHub tanto como a mí, puedes consultar la discusión sobre el algoritmo de reproducción aleatoria original que se busca para Eth2 aquí, donde se anuncia el ganador final.

Si desea ver el algoritmo de barajar de intercambiar o no desde otro ángulo, puede echar un vistazo a una explicación más visual publicada por Protolambda.

último

Esta imagen me muestra escuchando a Justin Drake hablar sobre cambiar o no barajar en EthCC en 2019, mientras implementaba la primera versión de cambiar o no barajar en el cliente de Teku (todavía se llamaba Artemis en ese momento). ☺

Autor | Ben Edgington

Tags：

MANA